熱力学のノート#２：第一法則からエントロピーへ
←熱力学のノート#１：熱、仕事、温度、そして永久機関 先日参加した熱力学の勉強会で学んだ内容を、自分なりに整理するために備忘録として残します。 ちなみに計算過程は省いて概要だけをまとめています。具体的な計算は別の記事でまとめています。スポンサーリンク
スポンサーリンク
熱力学の第一法則と第二法則
まず、熱力学の第一法則と第二法則から復習から…- 第一法則：エネルギー保存則であり、熱の定義式とみることもできます。内部エネルギーの変化は、熱と仕事の形で表され、式では以下のように表現されます。
$dU = d’Q + d’W$
ここで、$d’Q$と$d’W$の「’」は、熱や仕事が状態量ではないことを示してます。熱とは「仕事以外のエネルギー形態」と定義されるのでしたね。 ※状態量とは？ 『各状態で定義できる値』と『２状態の間にしたいしてのみ定義できる量』の２つがあります。 $U$や$T$や$P$など各状態で定義できる量を「状態量」と呼びます。 一方で$Q$や$U$や状態量ではありません。 状態量の特徴は「１、各状態ごとで定義できる」「２，経路に依存しない。つまり１周するとゼロになってしまう」の２つです。- 第二法則：熱効率を追求した結果、最高の熱効率は可逆サイクルで実現されるという主張。これは、「熱は自然には低温から高温には流れない」という経験則を法則にしたもので、熱機関の効率には根本的な限界があることを示しています。
カルノーサイクル
第二法則で最高の熱効率を持つとされる可逆サイクルのうち、最も単純なのがカルノーサイクルです。このサイクルは、4つの過程で構成されています。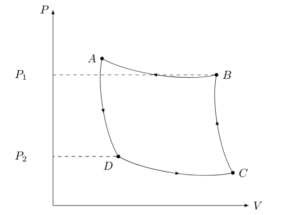
カルノーサイクルのPV図
- A→B：高温熱源($T_H$)から熱($Q_H$)を受け取りながら、等温膨張する。
- B→C：断熱膨張し、温度が$T_H$から$T_L$に下がる。
- C→D：低温熱源($T_L$)に熱($Q_L$)を放出しながら、等温圧縮する。
- D→A：断熱圧縮し、温度が$T_L$から$T_H$に戻る。
カルノーサイクルの熱効率とエントロピー
カルノーサイクルの熱効率($\eta$)は、外部にした仕事($W$)と受け取った熱($Q_H$)の比で定義されます。$\eta = W / Q_H = (Q_H – Q_L) / Q_H = 1 – Q_L / Q_H$
等温過程での理想気体の熱と仕事の関係、および断熱過程のポアソンの式を用いると、以下の関係式が導かれます。$\frac{V_B}{V_A} = \frac{V_C}{V_D}$
この関係式を熱効率の式に代入することで、カルノーサイクルの熱効率が温度だけで決まる式が導出されます。$\eta = 1 – T_L / T_H$
この式を変形すると、以下の関係式が得られます。$\frac{Q_H}{T_H} = \frac{Q_L}{T_L}$
実は、この導出された量 $\frac{Q}{T}$ こそがエントロピーなのです。（熱力学でのエントロピーの定義） 熱は状態量ではないですが、熱をその熱の移動が起きた時の絶対温度で割ったこの量は、状態量となるのです。つまり、ある状態から別の状態に移動する際の経路に依存しない量ということになります。この重要な状態量を、新たにエントロピー（$S$）と名付けたという流れです。
コメント