AIはなぜ言葉を理解できる？〜計算の観点から〜

あくまで個人的にまとめたノートなので、誤っている箇所があるかもしれません。参考にする際は内容の正当性について注意してください。もし誤っている箇所があればご指摘いただけたら嬉しいです。

AIは本当に、私たちの言葉を「理解」しているのでしょうか？

近年、ChatGPTのようなLLMの登場で、AIはまるで人間のように滑らかな文章を生成するようになりました。しかし、その裏側で一体何が起きているのか、ご存知でしょうか。

誤解を恐れずに言えば…

「AIは言葉を理解しているわけではありません。言葉を数値の「ベクトル」に変換し、その「距離」を計算しているだけなのです。」

私自身、学部生時代に人工知能を少しだけ研究の題材にしていました。当時はほんの基礎をかじった程度ですが、その時の学びが、今話題のLLM（大規模言語モデル）を理解する上で意外にも役に立つのではと気づきました。

そこで、専門家ではありませんが、私なりの言葉で「AIはどのように言葉を理解しているのか？」その仕組みを一緒に紐解いていきたいと思います。これから自然言語処理やLLMを学んでみたい方、そしてAIに少しでも興味がある方にとって、この記事が最初のきっかけとなれば嬉しいです。

そもそも「距離」ってなんだろう？
1. では、2次元の世界ではどうなるでしょう？
「ベクトル」で世界を表現する
モノを数値化する
言葉をベクトルにする
微分幾何学とAIの意外な関係
まとめ：AIは「距離」と「ベクトル」で言葉を理解する
1. 参考文献

そもそも「距離」ってなんだろう？

AIが言葉の意味をどう理解しているのか。その不思議な仕組みを紐解くには、まず数学的な「距離」という概念を理解することが欠かせません。

数学では、2つの点間の距離を引き算と絶対値を使って求めることができます。

補足：絶対値（▼をクリックすると隠れた項目が出てきます。）

絶対値は、「どれだけ離れているか」という純粋な大きさ（距離）を測るためのものです。数直線上で考えると、右向きの移動も左向きの移動も、同じ「距離」として扱えます。

例えば、数直線上にある2つの点A（位置 $x_A=2$）と点B（位置 $x_B=5$）の距離を考えます。

$$|x_B – x_A| = |5 – 2| = |3| = 3$$

次に、点Aと点Bの位置を逆にしてみましょう。

$$|x_A – x_B| = |2 – 5| = |-3| = 3$$

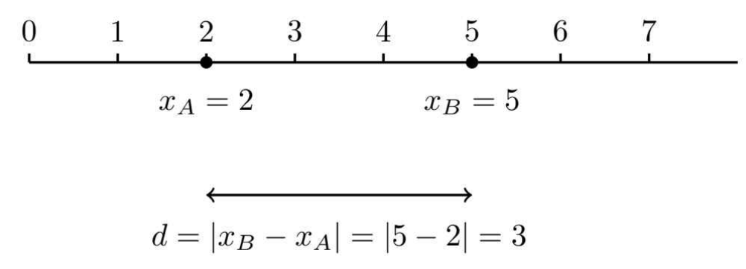
Figure‐A1：$|x_B – x_A| = |5 – 2| = |3| = 3$の模式図

このように、引き算の結果が正（右向き）でも負（左向き）でも、絶対値を取ることで常に同じ「距離」である3を得ることができます。絶対値は、引き算で生じる向きの情報（正負の符号）を消去し、純粋な大きさ、つまり距離だけの情報を取り出す働きをしています。

＜補足終わり＞

例えば、数直線上にある2つの点A（位置 $x_A$）と点B（位置 $x_B$）の距離 $d$ は、次のように表せます。

$$ d = |x_B – x_A| $$

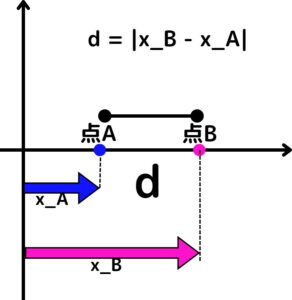
Figure1：$ d = |x_B – x_A| $の模式図

この考え方は、AIが物事の「近さ」を測るための基本中の基本となる考え方です。

では、2次元の世界ではどうなるでしょう？

たとえば、地図上の2つの地点の距離を考えるとき、東西方向の距離と南北方向の距離の両方を考慮する必要があります。このとき、単に引き算をするだけではうまくいきません。そこで登場するのが、三平方の定理（ピタゴラスの定理）です。

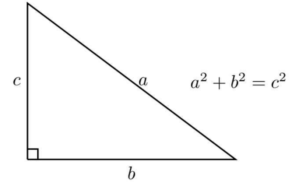
Figure2：三平方の定理（ピタゴラスの定理）の模式図

2次元平面上の点A $(x_A, y_A)$ と点B $(x_B, y_B)$ の距離 $d$ は、次のように求められます。

$$ d = \sqrt{(x_B – x_A)^2 + (y_B – y_A)^2} $$

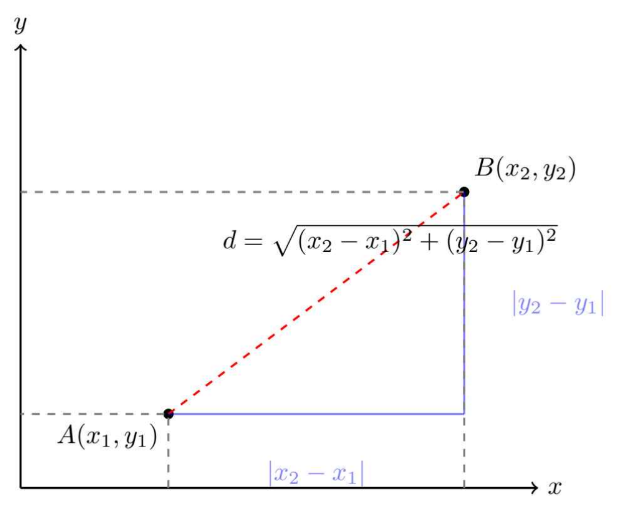
$Figure3：$ d = \sqrt{(x_B - x_A)^2 + (y_B - y_A)^2} $の模式図$

Figure3：$ d = \sqrt{(x_B – x_A)^2 + (y_B – y_A)^2} $の模式図

このように、次元が増えるにつれて「距離」の定義も拡張していくのです。この考え方が、AIが言葉を扱う際の鍵となります。

なぜ距離を求めるために平方根（ルート）が出てくるの？（▼をクリックすると隠れた項目が出てきます。）

なぜ距離を求めるために平方根（ルート）が出てくるの？

数学の世界では、符号（プラスやマイナス）を気にせず、純粋な「大きさ」だけを測りたい場面があります。

複数の数字を足し合わせて全体の大きさを知りたい時、プラスとマイナスの数が打ち消し合ってしまい、実際の大きさが正確に反映されないことがあります。この問題を解決するために、すべての数字を2乗して、負の符号を消してしまいます。（例:$(-3)^2=(−3)×(−3)=+9$）

しかし、これだけだと、数字が2乗された分だけ大きくなりすぎてしまいますね。そこで、2乗する前の元の大きさに戻すために、その逆の操作である平方根（ルート）をとるのです。

この方法は、特に物理学やデータサイエンスで、向きや方向を気にせず、全体の距離やばらつき具合を測りたいときによく使われます。

次の章では、この考え方をさらに高次元へと拡張し、ベクトルという概念を導入していきます。

「ベクトル」で世界を表現する

次に、ベクトルを考えます。これは「大きさ」と「向き」を持つ便利な量です。私たちが住む3次元空間は、3つの基底ベクトル（x軸、y軸、z軸）を使って、（範囲に制限がなければ）どんな点でも表現できます。

例えば、座標 $(x, y, z)$ は、基底ベクトル $\vec{i} = (1, 0, 0)$, $\vec{j} = (0, 1, 0)$, $\vec{k} = (0, 0, 1)$ を使って次のように表すことができます。

$$ (x, y, z) = x\vec{i} + y\vec{j} + z\vec{k} $$

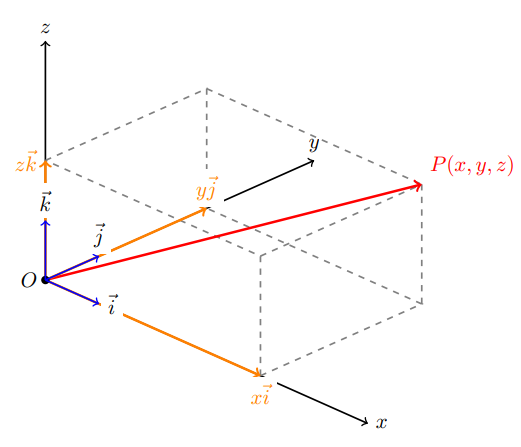
$Figure4：$ (x, y, z) = x\vec{i} + y\vec{j} + z\vec{k} $の模式図$

Figure4：$ (x, y, z) = x\vec{i} + y\vec{j} + z\vec{k} $の模式図

x,y,zに任意の数字を入れると、3次元のどの位置でも表せることが分かるでしょうか？
0を入れても構いません。例えば0を1つ入れると、基底ベクトルが1つ落ちて2次元になります。

この考え方を、もっと身近なものに当てはめてみましょう。

モノを数値化する

仮に、ある物体を「硬さ」「色」「重さ」という3つの要素で表現するとします。

これを対応表などを作り数値に置き換え、3次元のベクトルとして表すことができます。このとき、2つの物体AとBのベクトルをそれぞれ $\vec{A}$ と $\vec{B}$ とすると、両者の距離 $d$ は、ユークリッド距離として次のように計算できます。

$$ d = \sqrt{(x_B – x_A)^2 + (y_B – y_A)^2 + (z_B – z_A)^2} $$

この距離が近いほど、二つの物体は「似ている」と判断できます。

例えば、3つの物体S、L、Mを（「硬さ」、「色」、「重さ」）で表したとき、物体Sが（2,1,3）、物体Lが（2,1,5）、物体Sが（10,−8,4）という結果が得られたとしましょう。このとき重さは各々近い値ですが、硬さと色の数値を見てみると物体Sと物体Lで同じ値であるため、距離を求める際にも物体Sと物体Lは似ているのでは？と考えることができると思います。

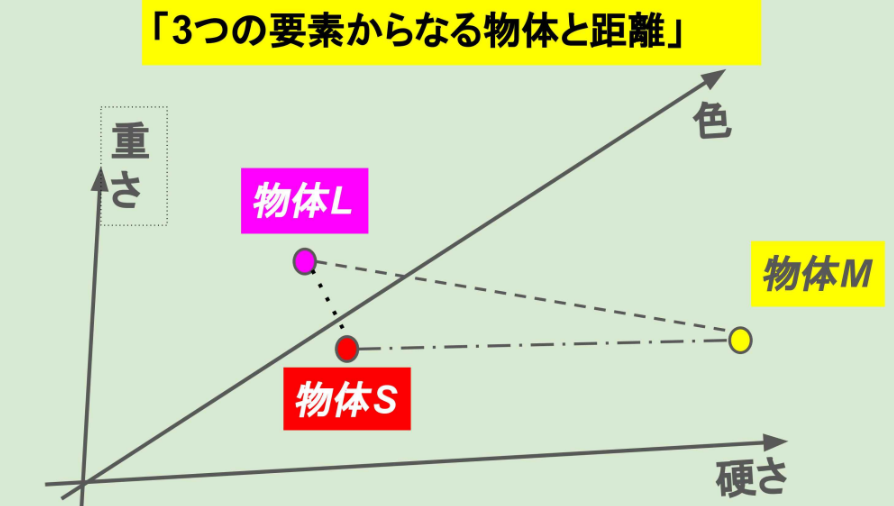
Figure5：3つの要素を持つ物体の模式図「物体SとLは、硬さと色が同じため、非常に近い。」

言葉をベクトルにする

この考え方は、言葉にも応用できます。AIは、単語や文を「何百、何千」という要素を持つベクトルに変換します。このベクトルのことを、埋め込み（Embedding）と呼びます。

例えば、「りんご」と「みかん」は、同じ「果物」という文脈を持つため、ベクトル空間上では非常に近い位置に配置されます。

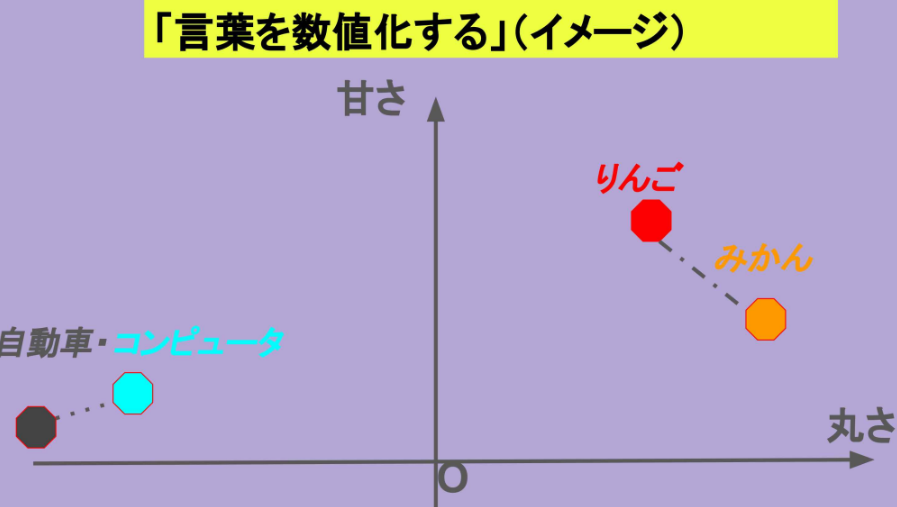
Figure6：2つの要素を持つ物体の模式図　「似た意味を持つ言葉は、ベクトル空間上で近い位置に配置される。あくまでイメージ図で配置は適当ですが、意味が近いと距離が近いことが分かると思います。」

そして、数値に対して任意の操作をしたときに、言葉の類似度がどのような変化をしていくのかが分かると、そこからも文脈がどの様になっているかを追うことができます。この操作も多くありますが、例えば「重要度の調整」や「意味の反転」などをみるとイメージが湧くのではないでしょうか？

重要度の調整: 特定の要素に大きな重みをつけることで、文脈の重要度を表現できます。例えば重要な要素があるなら、全てのベクトルのある要素の部分だけ100倍すれば注目することができますよね。
意味の反転: マイナスの値をかけることで、真逆の意味を持つ言葉（例：「良い」と「悪い」）を表現することも可能です。