熱力学備忘録:カルノーサイクルの熱効率導出
前回の熱力学の記事では概要だけで計算はあまり書いていませんでした。そこで勉強会の内容を元にカルノーサイクルの熱効率がどのように導出されるかを、計算過程を含めて詳細に振り返ることにします。熱効率の定義と基本式
カルノーサイクルの熱効率$\eta$は、高温熱源から受け取った熱$Q_H$に対する、系が外部にした仕事$W$の割合で定義されます。仕事は熱のやり取りの差分なので、以下の式で表されます。$\eta = \frac{W}{Q_H} = \frac{Q_H – Q_L}{Q_H} = – \frac{Q_L}{Q_H}$
熱量($Q_H, Q_L$)の計算
等温膨張(A→B)における熱量$Q_H$
等温過程では内部エネルギーの変化$\Delta U_{AB}$はゼロなので、$Q_H$は系が外部にした仕事$W_{AB}$に等しい。これを積分で計算しましょう。$Q_H = W_{AB} = \int_{V_A}^{V_B} P dV = \int_{V_A}^{V_B} \frac{nRT_H}{V} dV = nRT_H \ln\left(\frac{V_B}{V_A}\right)$
等温圧縮(C→D)における熱量$Q_L$
同様に、等温圧縮過程では$\Delta U_{CD}$はゼロなので、放出される熱量$Q_L$は外部からされた仕事$|W_{CD}|$に等しい。$Q_L = |W_{CD}| = \left|\int_{V_C}^{V_D} P dV\right| = \left|nRT_L \ln\left(\frac{V_D}{V_C}\right)\right| = nRT_L \ln\left(\frac{V_C}{V_D}\right)$
体積の関係式の導出
断熱過程のポアソンの式$PV^\gamma = \text{const.}$ と理想気体の状態方程式$PV=nRT$から、体積と温度の関係式$TV^{\gamma-1} = \text{const.}$ を用います。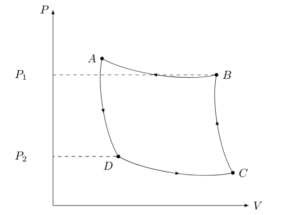
カルノーサイクルのPV図
- B→Cの断熱過程:$T_H V_B^{\gamma-1} = T_L V_C^{\gamma-1} \implies \frac{T_H}{T_L} = \left(\frac{V_C}{V_B}\right)^{\gamma-1}$
- D→Aの断熱過程:$T_L V_D^{\gamma-1} = T_H V_A^{\gamma-1} \implies \frac{T_H}{T_L} = \left(\frac{V_D}{V_A}\right)^{\gamma-1}$
$\left(\frac{V_C}{V_B}\right)^{\gamma-1} = \left(\frac{V_D}{V_A}\right)^{\gamma-1} \implies \frac{V_C}{V_B} = \frac{V_D}{V_A} \implies \frac{V_B}{V_A} = \frac{V_C}{V_D}$
熱効率の最終的な導出
熱効率の基本式に、先ほど求めた熱量$Q_H$と$Q_L$の式を代入し、体積の関係式$\frac{V_B}{V_A} = \frac{V_C}{V_D}$ を用います。$\eta = 1 – \frac{Q_L}{Q_H} = 1 – \frac{nRT_L \ln\left(\frac{V_C}{V_D}\right)}{nRT_H \ln\left(\frac{V_B}{V_A}\right)}$
$\frac{V_C}{V_D} = \frac{V_B}{V_A}$であるため、分子と分母の$\ln$の項が打ち消し合い、最終的な式が求まります。$\eta = 1 – \frac{T_L}{T_H}$






コメント