『勉強会カテゴリー/タグ』についての背景や取扱についてはリンク先をご覧ください.
※指数・対数の扱いにはこちらを参照してください。
数と単位
四則演算
数を計算する際には,足し算,引き算,掛け算,割り算の4つの計算方法があります.そして,それぞれの計算方法によって得られた結果を和,差,積,商といいました.
四則演算に関わる規則
- 計算は原則として左から行う
- 括弧のある計算では,括弧の中を先に計算する
- ×(掛け算)や÷(割り算)は,+(足し算)や-(引き算)よりも優先して先に計算する
四則演算に関わる規則が、しっかりと把握できていないと(30-16÷4÷2)などの計算で間違いが生じてしまいます.
数の分類
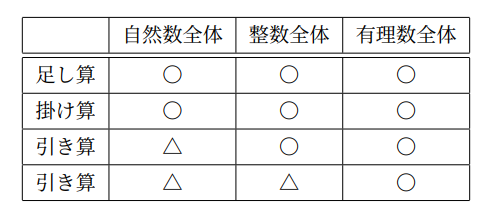
ものの個数を数えるために使われる数を”自然数” と呼びます.自然数の範囲では足し算と掛け算を自由に行うことができますが、引き算や割り算はできるとは限りません.
0や負数を加えることにより,引き算が自由に行えるようになります.0や負数を加えた数を”整数”と呼びます.しかし割り算はまだすべて扱えるわけではありません.
更に整数を分子・分母にもつ分数で表すことが出来る数を加えることで,割り算も自由に行うことができます.このような数を”有理数”と呼びます.
ここまでの内容を纏めておきましょう.
素数,循環小数
素数
割り算を行う際に,割り切る数を”約数”と呼びますが,「1とその数自身以外に約数を”持たない”2以上の自然数」を“素数”呼びます.
例えば,素数は2,3,5,7,11,13,17,19,23,29,31,…などがあります.
また,ある自然数をいくつかの素数の積の形で表すことを,その自然数の”素因数分解” といいます.素因数分解を最大限行うと表し方はただ一つしか存在しないことが知られています.
また,自然数の素因数分解に現れる素数を,特に“素因数”といいます.
循環小数
割り切れない分数($\frac{1}{3}$や$\frac{4}{13}$など)は,少数で表せば小数部分で繰り返していくことが知られています.
割り切れず小数部分が繰り返されるような小数を“循環小数”といいます.
単位
科学分野で使用される単位
日常でよく使われるのは,長さ($m$)、面積($m^2$)、体積($m^3$)、速さ($m/s$)等でしょうか.単位が揃っていない物理量は比較することができませんし,普段使わない単位を使うと量を想像するのが難しいでしょう.
ここで,科学分野にて使用される頻度の高い単位を纏めておきます.

コンピュータで使用される単位
コンピュータでは,0と1の2進数という数の表現が使用され,データも0と1の組み合わせで処理されています.
2進数の1桁のことをビット(bit)といい,コンピュータが利用できる情報の最小単位です.
コンピュータでは膨大な情報をやり取りするため,接頭語という大きな数や小さな数を分かりやすく表す表記があるので,ここで纏めておきましょう.
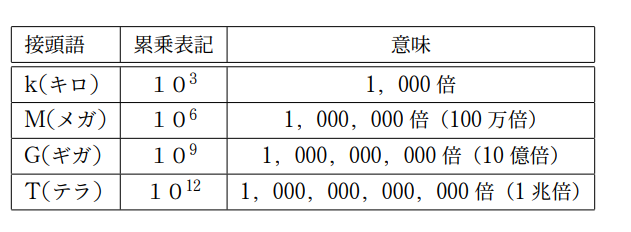
こちらは大きな数を表す接頭語です.数字の右上に小さな数字を書くことで,数字が何回かけられているかを表しています.例えば1,000の場合は$10×10×10$で3回10をかけているから、10の右上に3を書いて$10^3$となります.
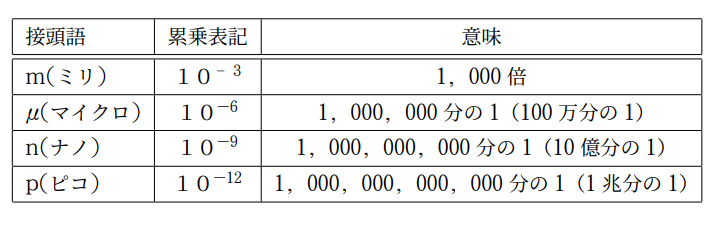
こちらは小さな数を表す接頭語です.数字の右上に小さな負数を書くことで,数字の逆数(つまりは「数字分の1」)を表しています.接頭語を知っていれば、数を扱いやすくなります.日常だと㎞(キロメートル)やkg(キログラム)という単位を使いますね.こちらはm(メートル)やg(グラム)の1,000倍の単位を扱っているのです.







コメント